Pianist: Scalable zkRollups via Fully Distributed Zero-Knowledge Proofs

Introduction

Pianist is a distributed zkSNARK protocol based on Plonk arithmetization that supports proof generation for general circuits with arbitrary connections. With multiple machines, both the prover time and the scalability can be improved linearly in the number of machines. More importantly, the communication between each machine and a master node is only constant, regardless of the size of the Plonk circuit. Both the proof size and the verifier time remain constant as well.

Pianist (Plonk vIA Non-limited dISTribution):

You shouldn't deploy Plonk only on a single machine, just like a pianist won’t play a great piece of music with only one finger.

In practice, our implementation shows that Pianist can generate the proof for $8192$ Rollup transactions (compiled by Circom) in just $313$ seconds on $64$ machines, while Plonk can only scale to $128$ transactions on one device with $300$ seconds of proving time. The communication per machine in Pianist is only $2.1$ KB, regardless of the number of transactions. The proof size is $2.2$ KB, and the verifier time is $3.5$ ms. Pianist has similar improvements for general circuits. On a randomly generated circuit with $2^{25}$ gates, it only takes $5$ s to create the proof using $32$ machines, $24.2\times$ faster than Plonk on a single machine.

The scheme is jointly developed by Tianyi Liu and Yupeng Zhang at University of Illinois Urbana-Champaign, Tiancheng Xie, Jiaheng Zhang and Dawn Song at UC Berkeley.

Key Advantages

Universal and updatable trusted setup. Pianist is based on the KZG polynomial commitment, which only requires a universal and updatable trusted setup.

Fully distributed achieving asymptotically optimal communication. Pianist enables distributed proof generation utilizing multiple machines, with only a constant communication on each machine. The scheme supports both data-parallel circuits and general circuits.

Plonkish arithmetization compatible. The implementation of Pianist is based on Plonk and is thus compatible with any Plonkish arithmetization.

Robustness. Pianist allows the master node to succinctly validate the messages received from each machine before merging them into the final proof for the whole circuit. This is especially helpful in the applications of zkRollup and zkEVM where the contributors of the proof may not be trusted.

Key ideas: Bivariate Plonk + Distributed KZG

The key technique in Pianist is a bivariate polynomial constraint system based on Plonk. We use the Lagrange polynomial of the second variable to combine the constraint on each machine together. This allows each machine to perform most of the computations locally, and only send a few constant-size messages in a constant number of rounds to the master node. The master node can then verify their correctness, and aggregate them to obtain the final ZKP proof. Taking the gate constraint in Plonk as an example:

Plonk gate constraint for Node i

g_i(X) := q_{a,i}(X)a_i(X) + q_{b,i}(X)b_i(X) + q_{o,i}(X)o_i(X) + q_{ab,i}(X)a_i(X)b_i(X) + q_{c,i}(X)

Bivariate Plonk constraint system

Suppose $s_i(X)$ is one of the witness columns from Node i, then we combine $s_0(X), \ldots, s_{M-1}(X)$ as:

S(Y, X) = \sum\nolimits_{i=0}^{M - 1}R_i(Y)s_i(X)

where $R_i(Y)$ is the $i$ -th Lagrange polynomial in terms of $M$ -th roots of unity. Then the constraints become:

G(Y, X) := Q_a(Y, X)A(Y, X) + Q_b(Y, X)B(Y, X) + Q_{ab}(Y, X)A(Y, X)B(Y, X) + Q_o(Y, X)O(Y, X) + Q_c(Y, X)

The constraint above can be proven in two steps. In the first step, $X$ is evaluated at a random point $\alpha$ , which can be computed locally on each machine together with a KZG proof:

S(Y, \alpha) = \sum\nolimits_{i=0}^{M - 1}R_i(Y)s_i(\alpha)

Each machine sends the evaluation $s_i(\alpha)$ together with the KZG proof to the master node, which can then verify their correctness and use them to compute the final proof. The protocol is shown below in Protocol 1.

By compiling the protocol with a bivariate KZG polynomial commitment scheme, we can build Pianist, a fully distributed SNARK. Please refer to our paper to see the full protocol and how to support general circuits.

Experiments

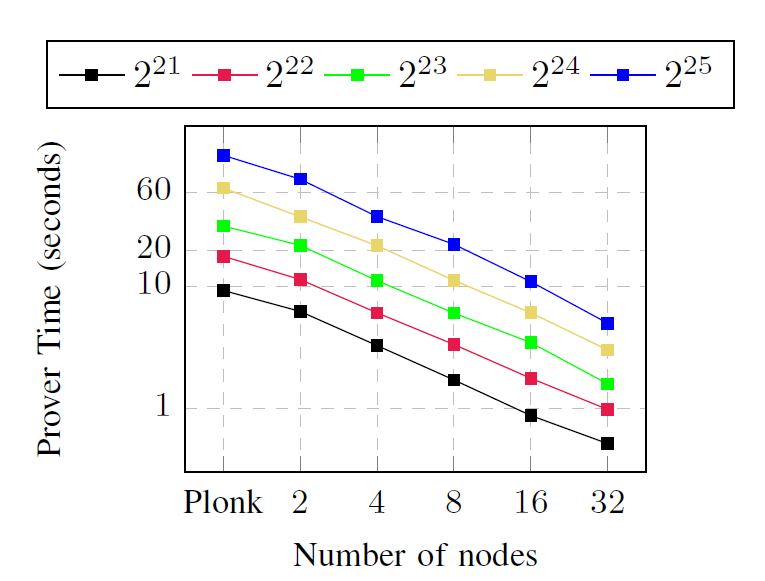
One of our experiments demonstrates that Pianist supports the distributed proof generation of general circuits with arbitrary connections. We vary the total size of the circuit from $2^{21}$ to $2^{25}$ , and randomly sample the type and the connection of each gate.

Proving time. As shown in the following figure, the running time is decreasing with the number of machines. In particular, for a random circuit of size $2^{25}$ , it takes $121$ s to generate the proof using Plonk on a single machine (with our optimizations), while it takes $76.9$ s on 2 machines in Pianist, $1.57\times$ faster than Plonk. It is further reduced to $5$ s using 32 machines, which is $24.2\times$ faster than Plonk.

Communication, proof size, and verifier time. The communication is $2336$ bytes per machine, the proof size is $2816$ bytes and the verifier time is $3$ ms